Optimal route planning at the touch of a button
There is currently a lot of talk about the fact that we all have to save much more energy, especially fossil energy. And even if it is of course the large companies whose efforts make the biggest difference, measures on a small scale can also make their contribution with their savings. Using an (admittedly highly simplified) example, we will show how, for example in the area of route planning, savings can also be made in small companies with mathematical optimization.
Routes are still planned based on empirical value; as the saying goes, based on our gut instinct. We have decided to use the example of an inner-city delivery service in order to demonstrate how you can optimize routes, lower your fuel costs and CO2 emissions as well as simulate strategic decisions (scenarios) using just a simple mathematical model. But let’s begin with route optimization first of all.
Our Example
Our delivery service supplies its customers on a daily basis and deploys a fleet of motor scooters in order to get around quickly in inner-city traffic. All of the drivers have been working for the company for several years now and know their way around quite well. This is why they mostly plan their tours themselves. However, the monthly accounting of the fuel receipts and log books shows that the fuel costs of the delivery service are extremely high. This means the routes will have to be planned by the manager in the future. However, manual planning is not only time-consuming; you also can’t be sure if it will yield an optimal result.
You can get the best result within a short time using mathematical optimization. Our delivery service decided to take part in the experiment and test automated route planning.
Considerable savings with little effort
You can achieve rapid success with just a basic optimization model which is entirely in line with the proverbial Pareto Principle, according to which you can achieve an 80% success rate with 20% effort. This applies in particular to our route planning example since the problem is fairly straightforward and can therefore be demonstrated with a very basic model.
The diagram shows the tours over the course of one day as driven by the delivery service so far.
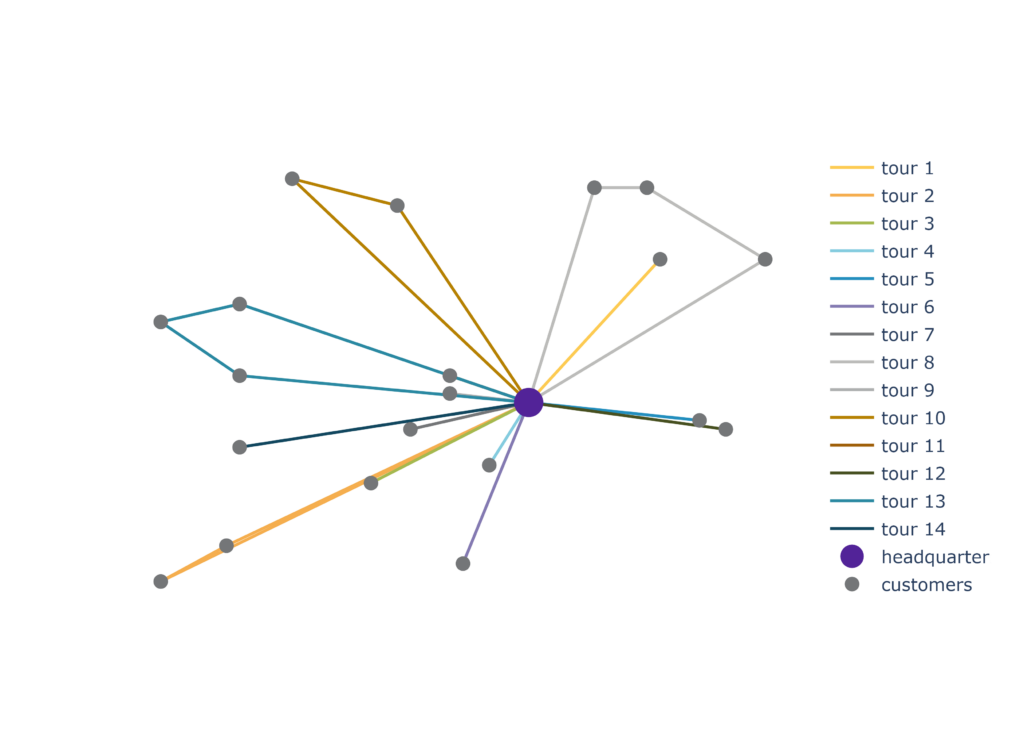
- Point: We can work out how expensive a specific route plan is;
- Point: We can note down all the important connections which constitute a route plan.
In general, mathematical optimization always works as follows:
- it develops any valid solution; in this case a route plan;
- it calculates how expensive the solution is;
- it looks for another solution which is less expensive.
Unfortunately there are so many possible solutions of this type that it would be impossible to count them all. Fortunately, this task can be assumed by special software – a so-called solver – which works with all sorts of scientific and practical tricks in order to find the best solutions in as clever and targeted a manner as possible.
Are you interested in our factsheet?
What are the benefits of mathematical optimization?
The solver does the searching
The route planning objective is clear: the length of all the routes per day should be as short as possible. The optimization target is therefore:
- (T1) The total length of all the routes has to be as short as possible.
- (D1) The connection of two locations on the map is either part of a route or not.
- (T1) The total length of all the routes should be as low as possible. Therefore we add together all the distances exactly when the connection of both locations is a part of the route (when the decision variable has the value 1)
- (C1) Exactly one driver supplies each customer.
- (C2) The driver then leaves the customer.
- (C3) All of the drivers set out from the headquarters.
- (C4) All of the drivers end their tour at the headquarters.
- (C5) The number of drivers you actually need depends on the number of scooters available.
- (C6) A sufficient number of drivers deliver to a random selection of customers to cover the requirements of the group selected.
Point C5 – one of the self-evident facts – can be extended to include a further target: do all the scooters really need to be in use?
- (D2) How many drivers are actually needed?
More interesting articles
In this interview, Lovis Anderson, Product Owner, talks about the new version of the OPTANO software solution for network optimization.
Is supply chain transformation a way towards differentiation in the highly competitive environment of the chemical industry?
Small and medium-sized companies encounter many challenges in their markets. Mathematical optimization can help to overcome these.
From a mathematical viewpoint, there may be better formulations. However, for a trial run of this problem at hand, this should be sufficient for now.
The model means you’re more than half-way
And after a few months the results are evident, not just in theory but in practice: fuel costs have definitely been reduced since planning the tours by automation every morning.
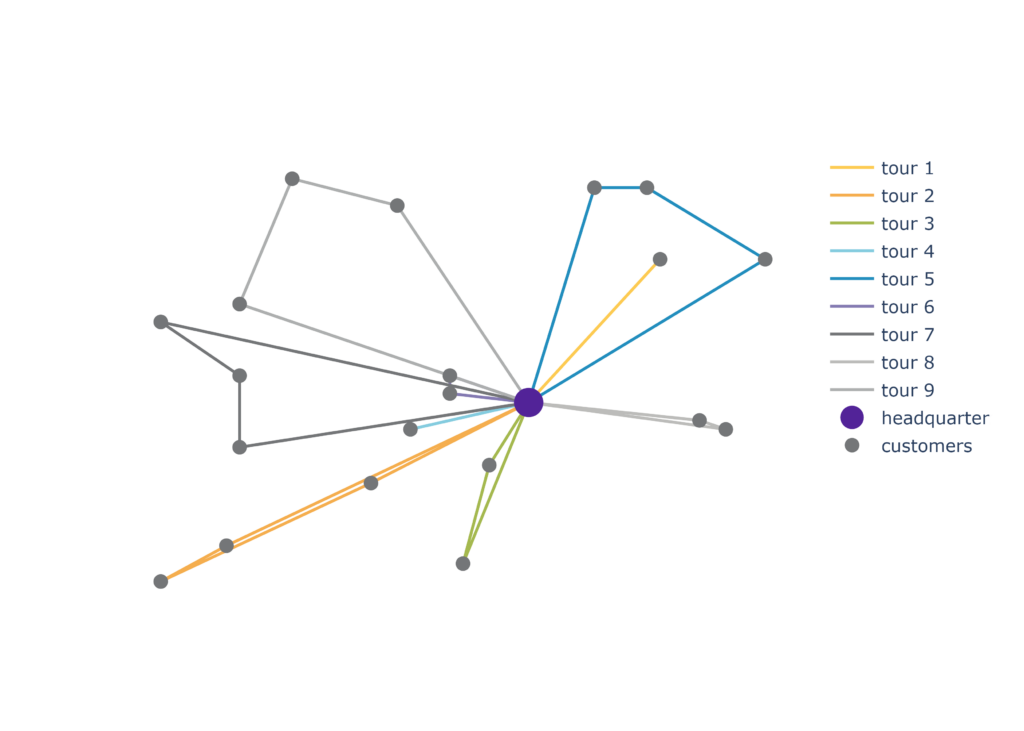
And after a few months the results are evident, not just in theory but in practice: fuel costs have definitely been reduced since planning the tours by automation every morning.
Manual planning
Basic planning
Difference
Number of tours
14
9
5
Length of tours
525,50 km
413,47 km
Costs per
day
€17,34
€13,64
€3,70
Costs per
year
€6329,70
€4980,20
€1349,50
Number of tours
Manual planning
14
Basic planning
9
Difference
5
Length of tours
Manual planning
525,50 km
Basic planning
413,47 km
Difference
112,04 km
Costs per day
Manual planning
€17,34
Basic planning
€13,64
Difference
€3,70
Costs per year
Manual planning
€6329,70
Basic planning
€4980,20
Difference
€1349,50
Of course, this is only a very abstract and theoretical example. However, we have made the experience over the years that considerable savings can almost always be achieved by optimizing such problems. In addition, if necessary, we can also add the minimization of CO2 emissions as an objective and optimize it further. There are many ways to save energy, let’s use them!
OPTANO can also be used to optimize much more complex scenarios and problems. We will be happy to advise you on whether the use of mathematical optimization is worthwhile for your company. Just contact us.
Have you already got your factsheet Factsheet on this topic?
In our factsheet “What are the benefits of mathematical optimization?” we ask 5 questions to help you assess whether mathematical optimization brings benefits to your organization.
To obtain our factsheet, all you need to do is enter your contact details in the space below. A pop-up window will then open to download the whitepaper. Please note that by providing us with your email address, you agree that we may contact you on this topic. You may revoke this agreement at any time by contacting [email protected].
powered by Borlabs Cookie