Optimale Tourenplanung auf Knopfdruck
Aktuell wird sehr viel darüber gesprochen, dass wir alle viel mehr, vor allem fossile Energie einsparen müssen. Und auch wenn es natürlich die großen Betriebe sind, deren Anstrengungen am meisten ausmachen, können auch Maßnahmen im kleinen Rahmen mit ihren Einsparungen ihren Teil beitragen. An einem (zugegeben stark vereinfachten) Beispiel zeigen wir, wie beispielsweise im Bereich der Tourenplanung auch in kleinen Betrieben mit mathematischer Optimierung gespart werden kann.
Touren werden vielfach noch auf Basis von Erfahrungswerten, also wie man so schön sagt, aus dem Bauch heraus geplant. Am Beispiel eines innerstädtischen Lieferservices wollen wir zeigen, wie man bereits mit einem einfachen mathematischen Modell Touren optimieren, Benzinkosten und CO2-Emissionen senken und strategische Entscheidungen simulieren kann (Szenarien). Fangen wir jedoch bei der Tourenoptimierung an.
Unser Beispiel
Unser Lieferservice beliefert seine Kunden täglich und nutzt dafür eine Flotte von Motorrollern, um im innerstädtischen Verkehr schnell voran zu kommen. Die Fahrer sind allesamt langjährig beim Unternehmen beschäftigt und verfügen über große Erfahrung. Daher planen Sie ihre Touren weitgehend selbstständig. Allerdings zeigt die monatliche Abrechnung der Tankquittungen und Fahrtenbücher, dass die Benzinkosten des Lieferdienstes enorm hoch sind. Die Touren sollen daher künftig zentral geplant werden. Eine manuelle Planung ist jedoch nicht nur zeitaufwändig, sondern man kann auch nicht sicher sein, dass die Planung auch ein optimales Ergebnis liefert.
Mit mathemathischer Optimierung kann man das jeweils beste Ergebnis in kurzer Zeit finden. Unser Lieferservice lässt sich auf das Experiment ein und testet die automatische Planung der Touren.
Viel gespart mit wenig Aufwand
Schon mit einem einfachen Optimierungsmodell lassen sich sehr schnell Erfolge erzielen, ganz im Sinne des sprichwörtlichen Pareto-Prinzips, laut dem man mit 20% des Aufwands bereits 80% des Erfolgs generieren kann. Das trifft insbesondere auf das aktuelle Beispiel der Tourenplanung zu, denn die Fragestellung ist recht übersichtlich und kann daher mit einer sehr einfachen Modellierung dargestellt werden.
Die Grafik zeigt beispielhaft die Routen eines Tages, wie sie bisher beim Lieferservice gefahren wurden.
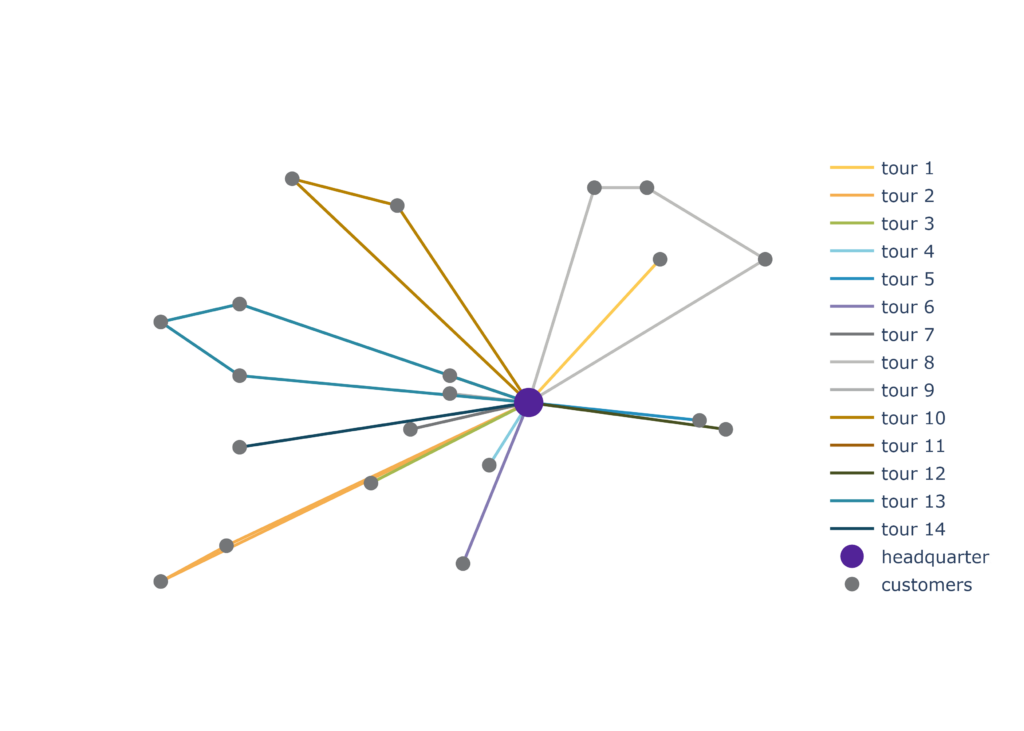
Das Problem der Tourenplanung erfüllt die beiden zentralen Voraussetzungen, um durch eine mathematische Optimierung lösbar zu sein:
- Punkt: Man kann für einen konkreten Tourenplan ausrechnen, wie teuer er ist;
- Punkt: Man kann alle wichtigen Zusammenhänge, die einen Tourenplan ausmachen, aufschreiben.
Eine mathematische Optimierung geht, allgemein gesprochen, immer wie folgt vor:
- sie entwickelt eine beliebige gültige Lösung, in diesem Fall einen Tourenplan;
- sie rechnet aus, wie teuer die Lösung ist;
- sie sucht eine andere Lösung, die günstiger ist.
Leider gibt es derart viele mögliche Lösungen, dass man sie unmöglich alle durchzählen kann. Glücklicherweise übernimmt diese Aufgabe Spezialsoftware, ein sogenannter Solver, der mit allen Tricks aus Wissenschaft und Praxis arbeitet, um möglichst geschickt und zielgerichtet nach den besten Lösungen zu suchen.
Interessieren Sie sich für unser Factsheet?
Was bringt mathematische Optimierung?
Die Suche übernimmt der Solver
Das Ziel der Routenplanung ist klar: die Länge aller Touren des Tages sollen so klein wie möglich gehalten werden. Das Ziel der Optimierung ist also:
- (T1) Die Summe der Länge aller Routen soll so klein wie möglich sein.
Dazu benötigt man insbesondere die Entscheidung darüber, was eine Route überhaupt ausmacht.
Ein echtes Optimierungsmodell beschreibt diesen Zusammenhang mathematisch. Dazu werden natürlich ein paar Daten als Parameter benötigt.
Als erstes gilt es, für jede mögliche Verbindung zwischen den Orten auf der Karte herauszufinden, ob sie Teil einer Tour sind oder nicht. Mathematisch entspricht das einer binären Variable, die also entweder den Wert „ja, das ist so“ (numerisch 1) oder „nein, so ist das nicht“ (numerisch 0) annehmen kann.
- (D1) Die Verbindung zweier Orte auf der Karte ist entweder Teil einer Tour oder sie ist es nicht.
- (T1) Die Summe der Länge aller Routen soll so klein wie möglich sein. Es werden also alle Distanzen genau dann aufsummiert, wenn die Verbindung zwischen den Orten Teil der Route ist (die Entscheidungsvariable also den Wert 1 hat).
- (C1) Jeder Kunde wird von genau einem Fahrer angefahren
- (C2) Der Fahrer verlässt den Kunden auch wieder
- (C3) Alle Fahrer, die eingesetzt werden, beginnen ihre Tour in der Zentrale
- (C4) Alle Fahrer, die eingesetzt werden, beenden ihre Tour in der Zentrale
- (C5) Es können nicht mehr Fahrer gleichzeitig eingesetzt werden, als Motorroller zur Verfügung stehen
- (C6) Jede beliebige Auswahl an Kunden wird von genug Fahrern angesteuert, um den Bedarf der ausgewählten Gruppe zu decken
- (D2) Wie viele Fahrer müssen tatsächlich eingesetzt werden
Weitere interessante Beiträge
Für Unternehmen sind Trade-offs alltägliche Realität und eine Herausforderung, die es zu meistern gilt.
Mathematische Optimierung kann in vielen Bereichen gewinnbringend eingesetzt werden: wir zeigen Ihnen, wie es funktioniert und ob das auch etwas für Ihr Unternehmen ist.
Wie können Unternehmen in der Medizintechnikbranche den richtigen Produktionsplan erstellen? Mathematische Optimierung könnte die Antwort sein…
Das Modell ist schon die halbe Miete
Ist das Modell erst da, geht der Rest sehr schnell. Die Kunden- und Bestelldaten liegen als Tabellen vor und können einfach übernommen werden. Dank der OPTANO Plattform kann das Modell in Null Komma nichts umgesetzt werden und zum ersten Mal eine automatische Tourenplanung gestartet werden.
manuelle Planung
Basisplanung
Differenz
Anzahl der
Touren
14
9
5
Länge der
Touren
525,50 km
413,47 km
Kosten pro
Tag
17,34 €
13,64 €
Kosten pro
Jahr
6329,70 €
4980,20 €
Anzahl der Touren
Manuelle Planung
14
Basisplanung
9
Differenz
5
Länge der Touren
Manuelle Planung
525,50 km
Basisplanung
413,47 km
Differenz
112,04 km
Kosten pro Tag
Manuelle Planung
17,34 €
Basisplanung
13,64 €
Differenz
3,70 €
Kosten pro Jahr
Manuelle Planung
6329,70 €
Basisplanung
4980,20 €
Differenz
1349,50 €
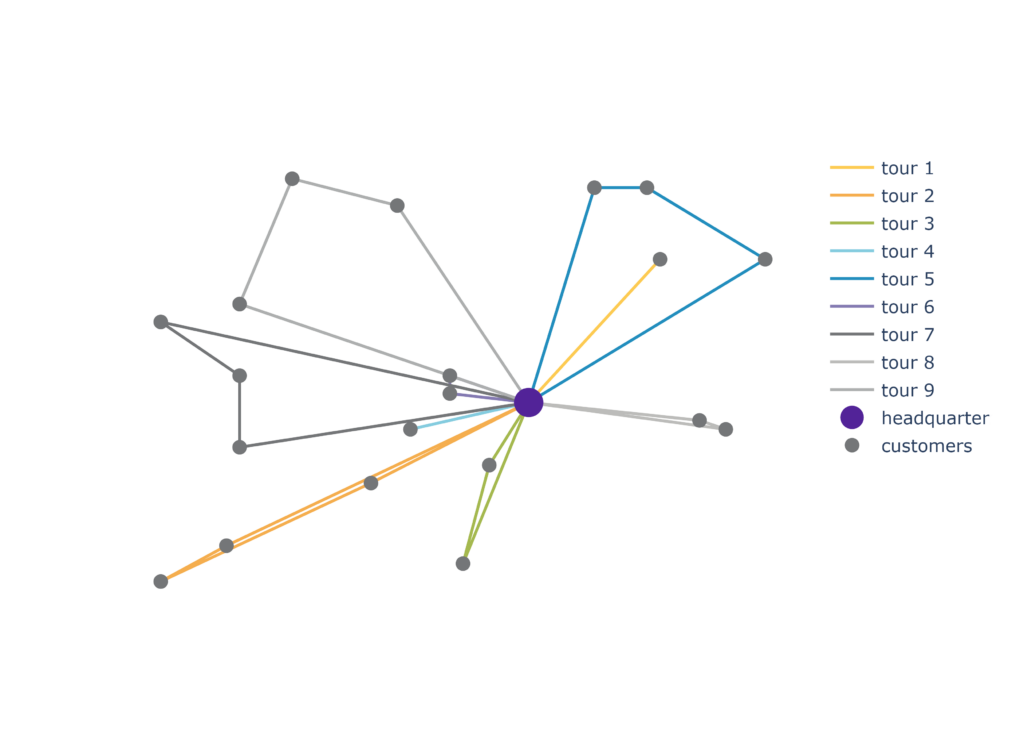
Und nach einigen Monaten zeigt sich auch in der Realität: Die Spritkosten sind deutlich zurückgegangen, seitdem die Touren jeden Morgen automatisch geplant werden.
Kennen Sie schon unser Factsheet zum Thema?
In unserem Factsheet Was bringt mathematische Optimierung? finden Sie Details zu den 5 obengenannten Fragen und können so Ihre persönlichen Anliegen und Probleme noch besser einordnen.
Um dieses Factsheet zu erhalten, müssen Sie nur Ihre Kontaktdaten in das untenstehende Formular eintragen. Es öffnet sich dann ein Pop-up-Fenster zum Downloaden des Whitepapers. Bitte beachten Sie, dass Sie mit der Angabe Ihrer E-Mail-Adresse zustimmen, dass wir Sie zu diesem Thema kontaktieren dürfen. Sie können diese Zustimmung jederzeit widerrufen, indem Sie sich an [email protected] wenden.
powered by Borlabs Cookie