What makes
a problem "complex"?
“So what exactly is it that you do?”
For years now this question has generally cropped up during small talk at family gatherings, parties or in the schoolyard with other parents while waiting to pick up our children.
And whenever I talk about my job, one word is mentioned significantly more than others. The word is complex. Because in order to describe what we do at OPTANO, I first have to explain what the problem is to which we have to find a
solution. My counterpart will frequently acknowledge my explanation with a nod because complex is a common
expression which is mostly used in connection with terms such as “multi-layered” or “comprising various aspects”. Yet, what does complex actually mean when it comes to problems? How can I determine whether a problem is complex or not?
What constitutes complexity?
The easiest answer to the questions as to whether a problem is complex or not would be: Can you find a solution easily and can you be sure that this solution is the best one? If this is not the case, then it is highly likely that you have a
complex problem on your hands. Of course, there are obvious factors which can contribute to the complexity of a
problem. We would like to clarify the individual aspects by using one example that we have confronted in many forms over the years: production planning. Bear in mind, however, that this problem can also be applied to other issues in
supply chain or logistics planning.
Complexity because of size
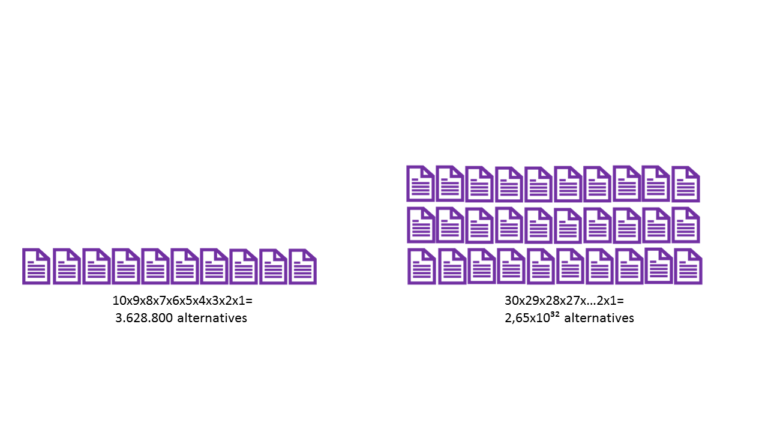
When we talk about the size of a problem we mean: How many possible solutions actually exist (the size of the solution space)? If a problem has so few solution alternatives that you have a clear overview of them all and can easily find them, then it is not complex. Only when there are so many possibilities that it is difficult to compare them and weigh them up against one another do you have a complex problem. Of course, humans have always tended to make incorrect estimations of the number of alternative solutions and believe the problem is easier to solve than it actually is. For example: We want to put 10 production jobs into a sequence. The first solution is easy to find: The jobs are processed in a random sequence, one after the other. However, since the set-up times differ because of the job sequence we cannot claim that every sequence is as good as the other. For this simple task alone, which consists of just 10 elements with one decision each (namely their position in the sequence), there are already 3,628,000 possible solutions. Nowadays, the fastest computer would need less than one second to calculate all the solutions. That is not really a problem, you might say. But now let us imagine there are 30 instead of 10 jobs and these “only” need to be put in order. While this does not actually sound as if it is soo much more – it is: There are 265,252,859,812,191,000,000,000,000,000,000 possible sequences. Even the fastest computer would need 150 million years to evaluate all the possible sequences! Now it is obvious why experimenting is not such a good strategy after all.
Complexity because of dependencies
One of the most important aspects when evaluating complexity is how decisions depend on each other. This means that changing one decision results in changes to all the other decisions. In this way, there is an entire chain of changes that need to be made and, at worst, a small change invalidates the solution because there is no longer a valid solution to the other changes.
In this respect, production planning is a very complex problem because everything is connected somehow. If you bring forward the production of a certain product by one day for scheduling reasons, then the necessary resources and machines are not available at that time. Therefore, you have to postpone the actual scheduled production. If other production processes are dependent on this one because the products are needed for it, then these also have to be postponed. And so an entire production plan often has to be changed.
Complexity caused by constraints
One example of constraints in production planning is the natural limitation of resources. If there were as many kinds of machines as there were orders, creating a production plan would be far easier. You wouldn’t have to worry about whether or not the plan could be implemented with the machines available. Each machine would immediately process its own job. Industrial machines are, of course, usually very expensive and purchasing them has to be worth it. This is why the number of machines is limited and thus the resources which are available for the production. (This is also similar in the case of consumer goods).
Complexity caused by conflicting goals
- minimum idle machine time
- low production costs
- few delivery delays
- low stock level
Complexity caused by change
Are you interested in our factsheet?
What are the benefits of mathematical optimization?
Optimal solutions with mathematical optimization
Even if we as humans can quickly lose track of things in complex problems, mathematical optimization does not. With state-of-the-art methods and algorithms it can find the best solution to any problem.
The mathematical model reflects all the relevant aspects of a problem and based on this model planning can be optimized with respect to different goals. In this way, you can also run through your strategic planning in what-if scenarios. Mathematical optimization can then make sound recommendations for action based on your available data.
Are your problems complex?
Complexity can be made up of various aspects. Sometimes, however, just one of these aspects is enough to make a problem complex.
If you are not sure whether your planning problem is complex or not, then the following five questions can be of help:
- Do you often have to reschedule in the middle of a running process?
- Are there many cross-dependencies in your company?
- Do you optimize towards one or more objectives?
- Do you consider it important to know how good your plans are?
- Do you often have to plan under uncertainty?
If you answered at least one of the above questions with “yes”, then you should seriously consider deploying mathematical optimization in your company.
More interesting articles
Wish lists, demand forecasts and production planning – a tongue-in-cheek glance into the toy factory of Santa’s elves.
If an urgent order comes in unexpectedly, it can turn everything on its head. Respond quickly and effectively with mathematical optimization.
High demands are placed on modern production networks. Mathematical optimization can help to meet them.
OPTANO - everything from a single source
Our OPTANO platform deploys the most sophisticated algorithms in mathematical optimization. In this way you obtain a sound basis for decision-making in order to find the best decisions for your planning challenges. OPTANO makes your planning process efficient, fast and flexible.
We continuously incorporate the experience we have gained from many different areas such as production planning, supply chain management, deployment and route planning as well as from various industries into our platform which is well-equipped to meet even the most specialized requirements.
In our factsheet What are the benefits of mathematical optimization? we explain more closely how mathematical
optimization works and how it can benefit your business. If you would like to learn more or would like to discuss specific problems with us, then contact us. We are glad to answer any of your questions about OPTANO and mathematical
optimization in your business. We look forward to your enquiry!
A complex example
Let us go back to the original question: “What do you do?” Of course I don’t explain what I do in as much detail as I have in this article. Normally I just give an example – mostly route planning with navigation devices because almost everybody has used these before and can understand what makes this problem a complex one.
Have you got your copy of our factsheet on this topic?
In our factsheet “What are the benefits of mathematical optimization?” we ask 5 questions to help you assess whether mathematical optimization brings benefits to your organization.
To obtain our factsheet, all you need to do is enter your contact details in the space below. A pop-up window will then open to download the whitepaper. Please note that by providing us with your email address, you agree that we may contact you on this topic. You may revoke this agreement at any time by contacting [email protected].
powered by Borlabs Cookie